Welcome to my blog! Unsure where to start?
- If you’re interested in math or theoretical CS, check out this post that explains a connection between random walks and bacteria growth. You might also like this post that talks about a paradox with the Halting Problem.
- If you’re into competitive programming, you might like this tutorial of a combinatorics problem. You can also check out the list of problems I’ve written for contests.
- If you like philosophy, here are my thoughts on the value of art, here is a metaphysical thought experiment, and here is my first and only attempt at writing sci-fi. Here is a longer piece about a new way to interpret probability.
Finally, if you enjoy any of these posts, consider subscribing to the Mailing List.
Suggested Posts
-
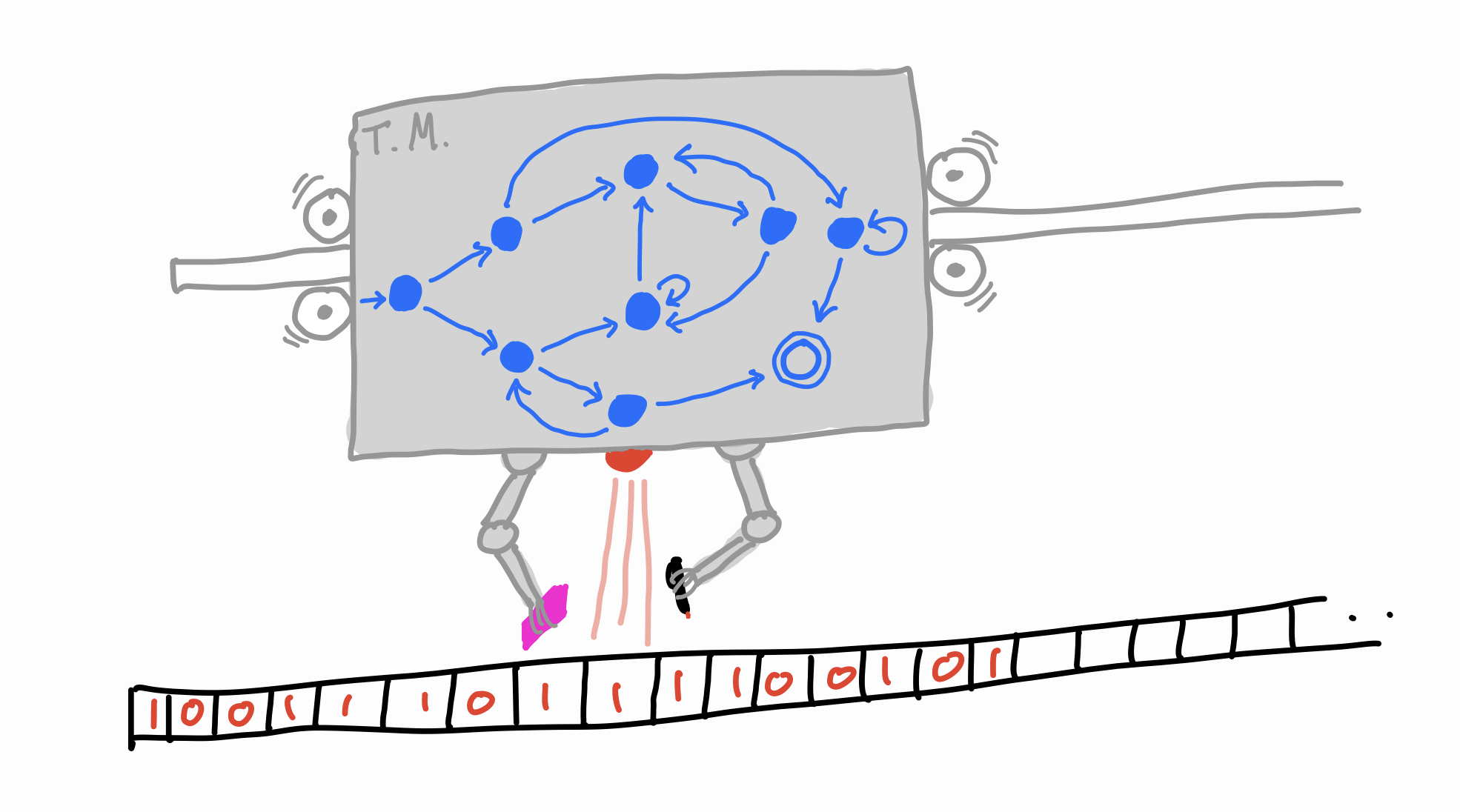
Theoretical Limitations of Autoregressive Models
Tags: artificial intelligence, computer science. 3200 words.
Chatbots that generate text autoregressively (like ChatGPT) have some important theoretical limitations.
Let's say you want to train an AI chatbot. It needs to be able to take in text (the user's question or instructions) and output text (its response). Intuitively you would think that the model, as a function $\phi$ from . . . -
Bacteria Growth and Random Walks
Tag: math. 1300 words.
We can represent a bounded random walk with parameter p as a branching process to calculate the moments of its stopping time.
A frog starts at position $k$ on the number line. Every second, it takes a hop to the right with probability $p$ and left with probability $1-p$. Let $T$ be the number of hops the frog takes before it reaches 0 for the first time . . . -
A Butterfly's View of Probability
Tags: math, philosophy. 3500 words.
Chaos theory provides an alternative to both the frequentist and Bayesian interpretations of probability.
What do we really mean when we use the word "probability"? Assuming that the universe obeys deterministic physical laws, an event must occur with either probability 0 or 1. The future positions of every atom in the universe are completely determined by their initial conditions. So what do we mean when we make statements like "Trump has a 25% chance of winning in 2024"? . . . -
The Value of Art
Tag: philosophy. 800 words.
Some brief thoughts on the way we value art.
I recently realized that I've been thinking about art -- especially modern art -- in the wrong way. Up until a few weeks ago, my biggest problem with modern art was that people try to extract too much meaning out of too little content. Can Rothko's painting of two fuzzy rectangles really capture the depths of human emotion? This seems to violate some law of conservation of . . . -
The Prometheus Simulation
Tags: philosophy, sci-fi. 2700 words.
A short story about creating life in a simulated universe.
Nine thousand Old-Earth years after the invention of Faster than Light travel, the physicist Marcus Dios imagined what would eventually become known as humanity's greatest science experiment. The Prometheus Simulation began as a seed in Dios's mind. It soon became a plan, then a project proposal, and finally a full project . . . -
The Periodic Box Problem
Tags: philosophy, physics. 1700 words.
A metaphysical thought experiment.
The entire universe consists of a rectangular box, which you are trapped in. Four of the faces -- the floor, the ceiling, and the left and right walls -- are solid metal and cannot be tampered with. However, the front and back faces (which are, say, 5 feet apart) act as portals . . .
All Posts (18)
-
Deduction-Projection Estimators for Understanding Neural Networks
Tags: artificial intelligence, computer science, math. 30000 words.
My undergraduate thesis on deductive estimation for machine learning.
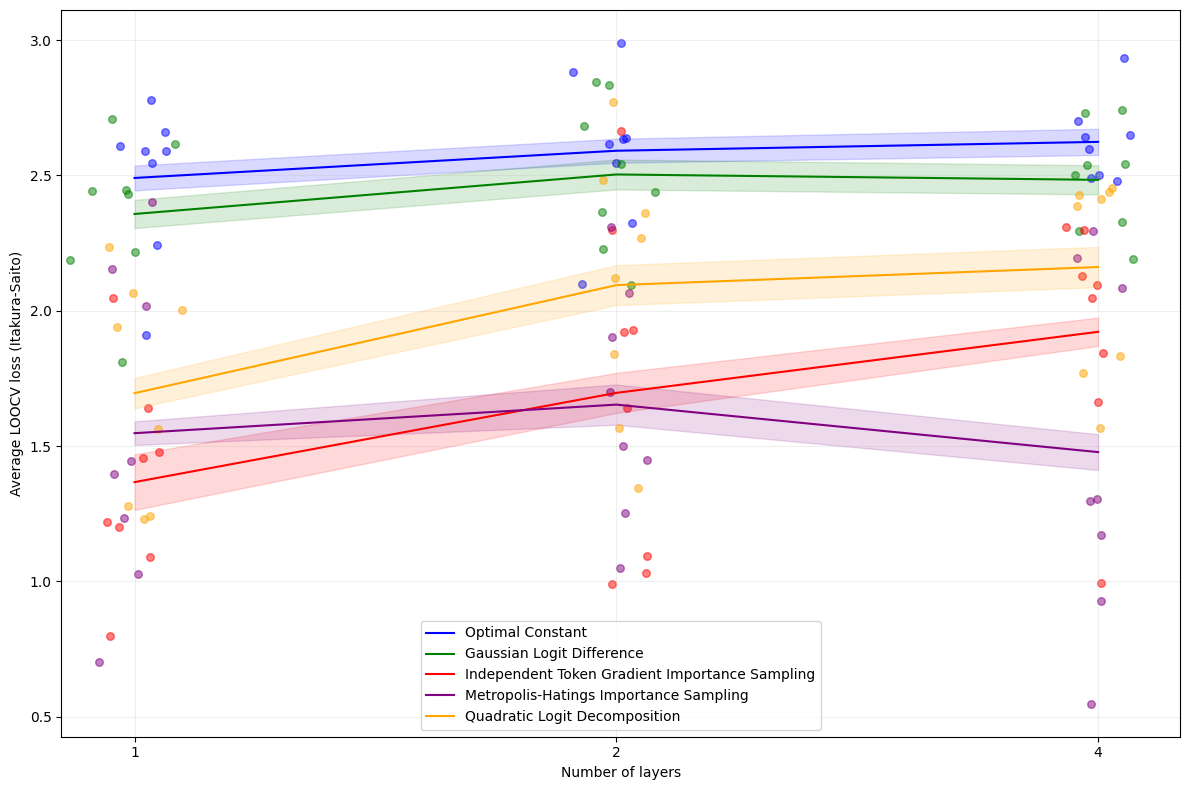
Abstract. We introduce Deduction-Projection Estimators: a family of methods for measuring properties of neural networks inspired by the notion of a “deductive heuristic estimator” introduced in Christiano et al. (2022). Unlike traditional techniques used in machine learning, a DPE produces its estimate by mechanistically tracking how activations are processed throughout a neural network. This allows us to understand how a model behaves over an entire input distribution without having to generalize from observed behavior on a finite number of sampled inputs . . .
-
Low Probability Estimation in Language Models
Tag: artificial intelligence. 2600 words.
A crosspost of work done at the Alignment Research Center. Redirects to alignment.org.
ARC recently released our first empirical paper: Estimating the Probabilities of Rare Language Model Outputs. In this work, we construct a simple setting for low probability estimation — single-token argmax sampling in transformers — and use it to . . .
-
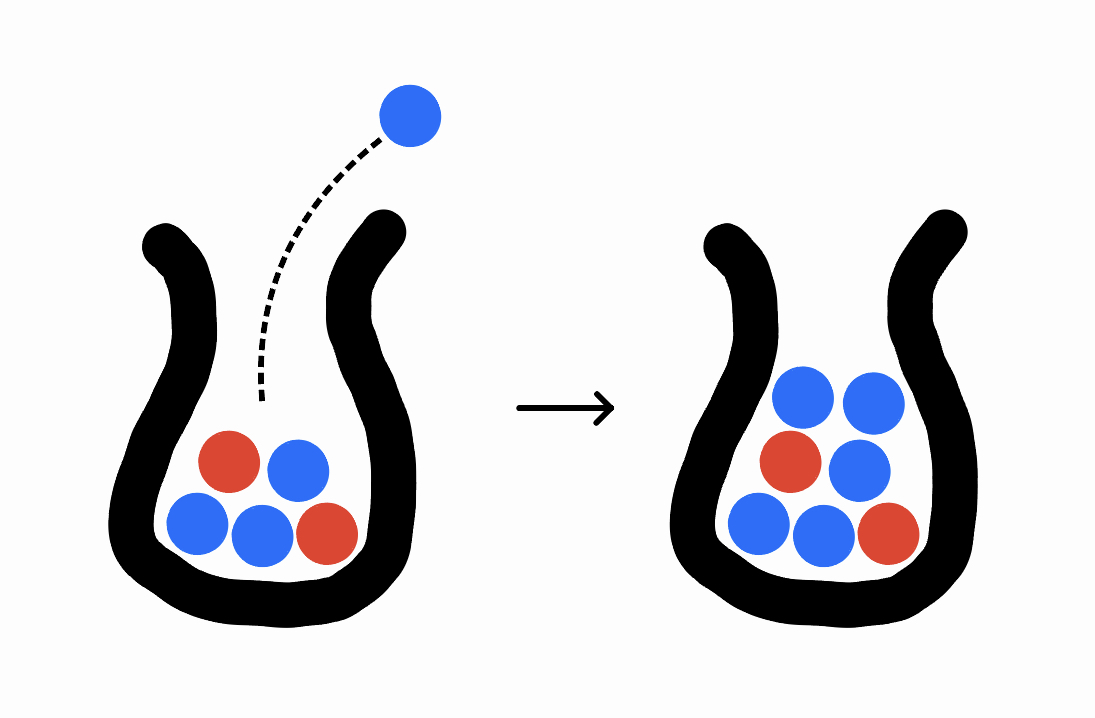
Polya's Urn with Bayesian Updating
Tag: math. 900 words.
Shedding light on an elegant interpretation of a classic statistical process.
Polya has an urn that starts out with one blue ball and one red ball. Every day, he draws a random ball from the urn, duplicates it, then returns both copies . . .
-
Theoretical Limitations of Autoregressive Models
Tags: artificial intelligence, computer science. 3200 words.
Chatbots that generate text autoregressively (like ChatGPT) have some important theoretical limitations.
Let's say you want to train an AI chatbot. It needs to be able to take in text (the user's question or instructions) and output text (its response). Intuitively you would think that the model, as a function $\phi$ from . . .
-
Reviews: Love Death + Robots
Tag: reviews. 1500 words.
My review of every episode of Love Death + Robots.
For the unaware, Love Death + Robots is a Netflix series of animated sci-fi/horror/fantasy short stories. I love this show for the same reason I love Ted Chiang stories . . .
-
Bacteria Growth and Random Walks
Tag: math. 1300 words.
We can represent a bounded random walk with parameter p as a branching process to calculate the moments of its stopping time.
A frog starts at position $k$ on the number line. Every second, it takes a hop to the right with probability $p$ and left with probability $1-p$. Let $T$ be the number of hops the frog takes before it reaches 0 for the first time . . .
-
A Butterfly's View of Probability
Tags: math, philosophy. 3500 words.
Chaos theory provides an alternative to both the frequentist and Bayesian interpretations of probability.
What do we really mean when we use the word "probability"? Assuming that the universe obeys deterministic physical laws, an event must occur with either probability 0 or 1. The future positions of every atom in the universe are completely determined by their initial conditions. So what do we mean when we make statements like "Trump has a 25% chance of winning in 2024"? . . .
-
The Geometry of Adversarial Perturbations
Tag: artificial intelligence. 2400 words.
Small changes to an image can trick many deep neural network classifiers. What does this say about the geometry of the classification space?
In this post, I want to briefly cover the results of the 2017 paper "Universal adversarial perturbations", and discuss what it implies about the geometry of classification boundaries. I hope to make this post accessible to readers who are new to machine learning, so I will not assume any prior knowledge beyond a general math background . . .
-
A Lower Bound on the Probability of Skeptical Scenarios
Tag: philosophy. 2500 words.
No matter how contrived a skeptical scenario is, the fact that you were able to think of it gives a constant lower bound on its likelihood.
Attaining true knowledge is hard. As far as I know, I could be a brain in a vat with my nerve endings connected to wires that are simulating physical experiences. Gravity could reverse directions every 13.8 billion years, the first time being tomorrow. Or, our entire universe could be a simulation . . .
-
The Smallest Number That Can't Be Described in 20 Words
Tags: computer science, math. 2400 words.
We examine a classic paradox: what's the smallest positive integer that cannot be described in 20 words or less? With a bit of formalization, this problem leads us to an alternate proof that the halting function is uncomputable.
Consider the set $S$ of all positive integers that can be completely described in 20 words or fewer. This set contains a lot of numbers. For example, "two to the power of ten" describes 1024 in six words. "One hundred and seven" describes 107 in four words . . .
-
The Value of Art
Tag: philosophy. 800 words.
Some brief thoughts on the way we value art.
I recently realized that I've been thinking about art -- especially modern art -- in the wrong way. Up until a few weeks ago, my biggest problem with modern art was that people try to extract too much meaning out of too little content. Can Rothko's painting of two fuzzy rectangles really capture the depths of human emotion? This seems to violate some law of conservation of . . .
-
The Prometheus Simulation
Tags: philosophy, sci-fi. 2700 words.
A short story about creating life in a simulated universe.
Nine thousand Old-Earth years after the invention of Faster than Light travel, the physicist Marcus Dios imagined what would eventually become known as humanity's greatest science experiment. The Prometheus Simulation began as a seed in Dios's mind. It soon became a plan, then a project proposal, and finally a full project . . .
-
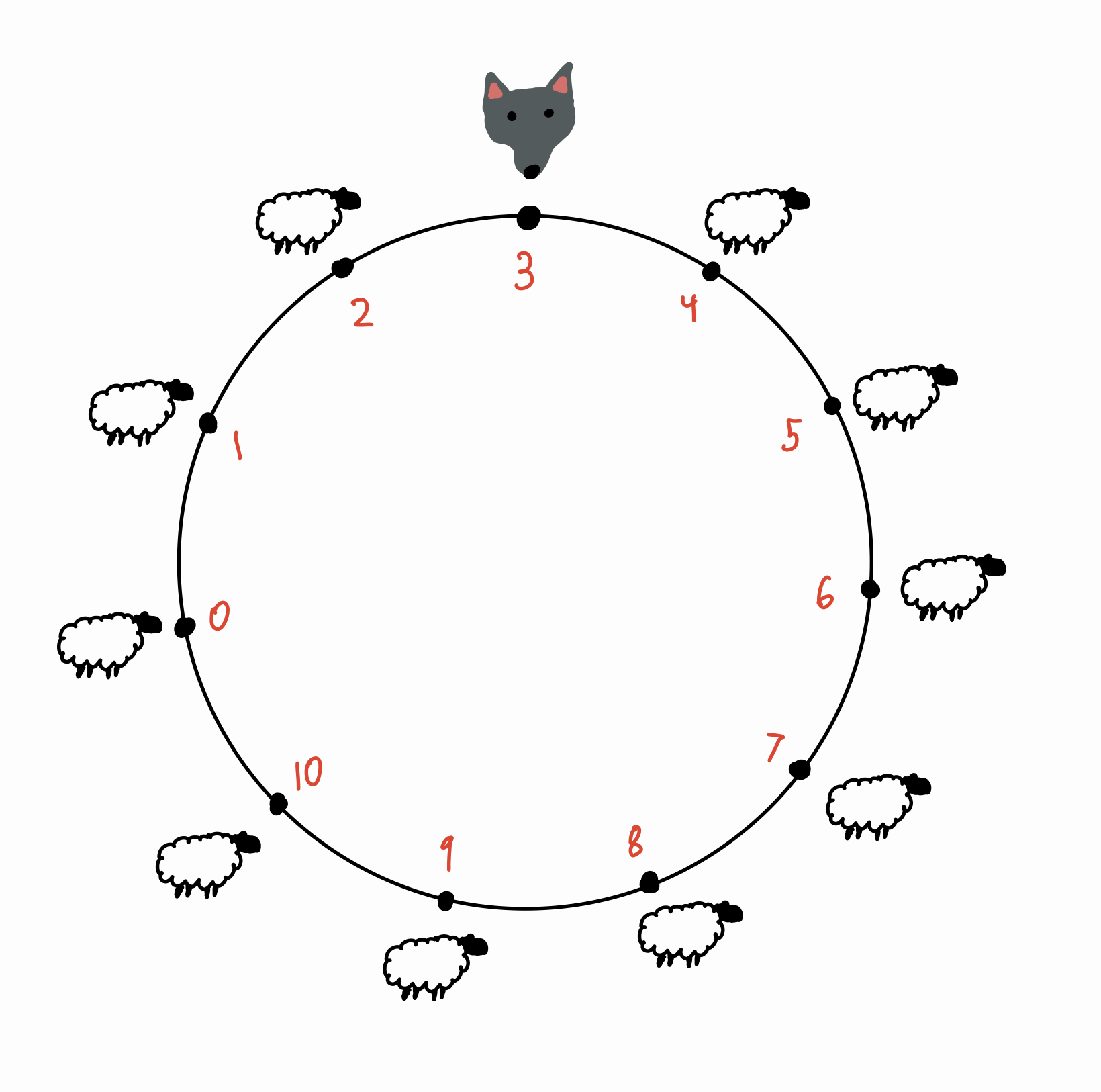
The Bounded Random Walk, Four Different Ways
Tag: math. 1600 words.
What is the probability that a random walk starting at 3 reaches 10 before 0?
Expected value (together with probability) is my favorite mathematical tool. One of the most appealing qualities of an expected value problem is that there are so many different ways of reaching the same answer. I want to demonstrate this conceptual fluidity with a standard problem. Say you're currently at position 3 on . . .
-
How to Survive Your First Semester at Harvard
Tag: serious. 500 words.
Here are four key steps you can take to survive your first few months of college.
I recently finished my first semester at Harvard. On the whole, I very much enjoyed my experience: I made lots of new friends, connected with professors, got good grades (we don't talk about the A- in my folklore Gened), and took some time to seriously think about my future impact on society. Looking back, I can identify some key steps I took that helped me stay afloat . . .
-
Flipping Coins
Tags: computer science, math. 3000 words.
What's the expected value of the number of times you must flip a coin before you encounter a given string, such as "HTTH"? Here's an algorithm to compute it.
A common initial (incorrect) intuition about this problem is that all strings of length n should have the same answer -- something like $2^n$. We sense that there should be some sort of symmetry between heads and tails, so it feels odd that "HHHH" should appear any earlier or later than "HTHT" . . .
-
The Periodic Box Problem
Tags: philosophy, physics. 1700 words.
A metaphysical thought experiment.
The entire universe consists of a rectangular box, which you are trapped in. Four of the faces -- the floor, the ceiling, and the left and right walls -- are solid metal and cannot be tampered with. However, the front and back faces (which are, say, 5 feet apart) act as portals . . .
-
Epistemic Context and Conditional Confidence
Tag: philosophy. 2100 words.
There are unspoken assumptions that accompany any statement of knowledge. This allows us to be skeptical about fundamental properties of the universe while still having confidence in everyday facts.
In Meditations, Descartes argues that we cannot fully trust the information given to us by our senses, as they have misled us in the past. We will never be able to rule out the possibilities that we are dreaming, that we are a brain in a vat, or that the universe (and all of our memories) sprang into existence 15 minutes ago. I find Descartes' argument compelling . . .
-
Automated Theorem Proving in Intuitionistic Propositional Logic
Tags: computer science, math, philosophy. 4000 words.
My high school Senior Research Project on designing algorithms to search for constructive proofs of logic theorems.
Abstract. Automated theorem proving uses algorithms to search for mathematical proofs. This paper describes three original theorem provers that operate in a branch of logic that lacks the law of excluded middle ($P \vee \neg P$), called intuitionistic propositional logic. One prover employs a randomized depth-first search (DFS) to construct a proof tree, another uses DFS with memoization, and the third uses a DFS in LJT sequent calculus . . .